무어 펜로즈 유사 역행렬이란 무엇인가?
행렬에 대해 역행렬을 구하기 위해서는 행렬이 비특이 행렬(non-singular matrix)이어야 한다. 만약 특이행렬이라면 역행렬이 없기 때문에 역행렬을 구할 수 없다.
역행렬을 구할 수 없는 상황을 해결하기 무어 펜로즈 유사 역행렬이 생겼으며, 어떤 $m \times n$ 행렬 $\mathbf{X}$에 대해 다음 네가지 조건을 만족하는 행렬을 $\mathbf{X}$의 유사역행렬 $\mathbf{X}^+$라 부른다.
1. $\mathbf{X} \mathbf{X}^+ \mathbf{X} = \mathbf{X}$
2. $\mathbf{X}^+ \mathbf{X} \mathbf{X}^+ = \mathbf{X}^+$
3. $(\mathbf{X} \mathbf{X}^+)^T = \mathbf{X} \mathbf{X}^+$
4. $(\mathbf{X}^+ \mathbf{X})^T = \mathbf{X}^+ \mathbf{X}$
무어 펜로즈 유사 역행렬이라는 단어가 길기 때문에 아래서 부터는 '유사 역행렬'으로 줄여 부른다.
유사 역행렬 계산하기
계산 방법 알아보기
앞서 다룬 특이값 분해를 사용해 $\mathbf{X}$에 대한 유사 역행렬을 계산할 수 있다. 특이값 분해에 대한 수식은 다음과 같다.
$$\mathbf{X} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^T$$
$\mathbf{U}$ : $m \times m$ 정사각 행렬로, $\mathbf{X}$의 좌특이 벡터(Left Singular Vectors)로 구성돼 직교 행렬이 된다
$\mathbf{\Sigma}$: $m \times n$ 대각 행렬
$\mathbf{V}$: $n \times n$ 정사각 행렬로, $\mathbf{X}$의 우특이 벡터(Left Singular Vectors)로 구성돼 직교 행렬이 된다.
만약 특이값 분해에 대해 잘 모른다면 아래 글을 먼저 보고 오면 된다.
특이값 분해(Singular Value Decomposition)란 무엇인가? PyTorch, TensorFlow, Numpy 사용해 특이값 분해하기
특이값 분해란 무엇인가?특이값 분해(Singular Value Decomposition, SVD)란 $m x n$ 차원의 행렬을 대각화해 세 개의 행렬로 분해하는 방법이다. 고유값 분해와 비슷하지만, 고유값 분해는 정사각 행렬에만
simplecode.kr
이렇게 $\mathbf{U}$, $\mathbf{\Sigma}$, $\mathbf{V}$를 구했으면 유사 역행렬 $\mathbf{X}^+$은 다음 수식으로 구할 수 있다.
$$\mathbf{X}^+ = \mathbf{V} \mathbf{\Sigma}^+ \mathbf{U}^T$$
아마 나머지 수식은 이해가 가는데 $\mathbf{\Sigma}^+$를 구하는 방법이 궁금할 것이다. $\mathbf{\Sigma}^+$는 $\mathbf{\Sigma}$와 내적했을 때 단위 행렬이 나오는 유사 역행렬으로, 대각 행렬이기 때문에 단순히 $\mathbf{\Sigma}$의 각 원소에 역수를 취한 후 전치(Transpose)를 해서 구할 수 있다.
예를 들어 다음 행렬에 대한 유사 역행렬은
$$\begin{bmatrix}
1 & 0 \\
0 & 2 \\
0 & 0
\end{bmatrix}$$
다음 행렬이 된다.
$$\begin{bmatrix}
1 & 0 & 0 \\
0 & 1/2 & 0 \\
\end{bmatrix}$$
이제 구하는 방법을 알았으니, 각 과정을 코드를 통해 알아보자.
코드로 계산하기
이 코드에서는 다음 행렬 $\mathbf{X}$에 대한 유사 역행렬을 구해본다.
$$\begin{bmatrix}
1 & 2 \\
-1 & 2 \\
0 & 1
\end{bmatrix}$$
1. 먼저 특이값 분해를 실행해 $\mathbf{U}$, $\mathbf{\Sigma}$, $\mathbf{V}$를 구한다.
X = np.array([[1, 2], [-1, 2], [0, 1]])
U, Sigma, VT = np.linalg.svd(X)
2. $\mathbf{\Sigma}^+$를 구하기 위해 $\mathbf{\Sigma}$를 대각 행렬로 만들고, 역수를 취한 다음 오른쪽에 0을 더한다.
Sigma_diag = np.diag(Sigma) ## 대각행렬 만들기
print("sigma_diag:\n",Sigma_diag)
Sigma_diag_inv = np.linalg.inv(Sigma_diag) ## 역수 취하기
print("Sigma_diag_inv:\n",Sigma_diag_inv)
Sigma_plus = np.concatenate((Sigma_diag_inv, np.array([[0, 0]]).T), axis=1) ## 오른쪽에 0 더하기
print("Sigma_plus:\n",Sigma_plus)
위의 코드를 실행해보면 다음과 같은 출력이 나온다.

3. 이제 $\mathbf{X}^+ = \mathbf{V} \mathbf{\Sigma}^+ \mathbf{U}^T$를 통해 $\mathbf{X}^+$를 구해보자.
X_plus = np.matmul(VT.T, np.matmul(Sigma_plus, U.T))
print(X_plus)
그러면 다음과 같은 결과가 나온다. 다음 행렬이 $\mathbf{X}^+$이다.

유사 역행렬이 구해졌다. 이 방법은 과정을 상세화 해서 조금 복잡하게 느껴질 수 있다. 이런 복잡성을 해결하기 위해 Numpy, TensorFlow, PyTorch 같은 머신 러닝 라이브러리에서는 유사 역행렬을 쉽게 구할 수 있는 방법을 제공한다.
Numpy, TensorFlow, PyTorch 사용해 유사 역행렬 구하기
Numpy 사용해 유사 역행렬 구하기
Numpy를 사용해 유사 역행렬을 구하기 위해서는 linalg.pinv 함수를 사용하면 된다.
import numpy as np
# 행렬 X 정의
X = np.array([[1, 2], [-1, 2], [0, 1]])
# 유사역행렬 계산
X_pseudo_inverse = np.linalg.pinv(X)
print("Numpy Pseudoinverse:\n", X_pseudo_inverse)
그러면 결과가 다음과 같이 나오는 것을 볼 수 있다.

우리가 위에서 구한 값과 완전히 동일한 것을 볼 수 있다.
TensorFlow 사용해 유사 역행렬 구하기
TensorFlow를 사용해 유사 역행렬을 구하기 위해서는 linalg.pinv 함수를 사용하면 된다.
import tensorflow as tf
# 행렬 X 정의
X = tf.constant([[1, 2], [-1, 2], [0, 1]], dtype=tf.float32)
# 유사역행렬 계산
X_pseudo_inverse = tf.linalg.pinv(X)
print("TensorFlow Pseudoinverse:\n", X_pseudo_inverse)
이 결과도 위와 동일한 것을 볼 수 있다.

PyTorch 사용해 유사 역행렬 구하기
PyTorch를 사용해 유사 역행렬을 구하기 위해서는 linalg.pinv 함수를 사용하면 된다.
import torch
# 행렬 X 정의
X = torch.tensor([[1, 2], [-1, 2], [0, 1]], dtype=torch.float32)
# 유사역행렬 계산
X_pseudo_inverse = torch.linalg.pinv(X)
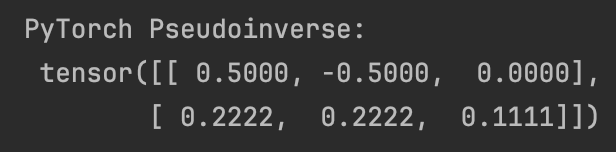
print("PyTorch Pseudoinverse:\n", X_pseudo_inverse)
결과값이 마찬가지로 동일한 것을 볼 수 있다.
'Machine Learning Math > Linear Algebra' 카테고리의 다른 글
| 특이값 분해(Singular Value Decomposition)란 무엇인가? PyTorch, TensorFlow, Numpy 사용해 특이값 분해하기 (0) | 2024.08.16 |
|---|---|
| 고윳값 분해(Eigen Decomposition) 란 무엇인가? Numpy, TensorFlow, PyTorch 사용해 고유값 분해 해보기 (0) | 2024.08.06 |
| 고유 벡터(Eigenvector)와 고유 값(Eigenvalue)이란 무엇인가? Numpy, TensorFlow, PyTorch로 고유 벡터 구해보기 (0) | 2024.08.02 |
| 아핀 변환(Affine Transformation)이란 무엇인가? (0) | 2024.08.01 |
| 직교 행렬(Orthogonal Matrix)이란 무엇인가? (0) | 2024.07.31 |

